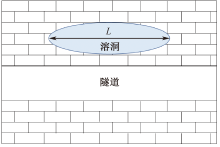
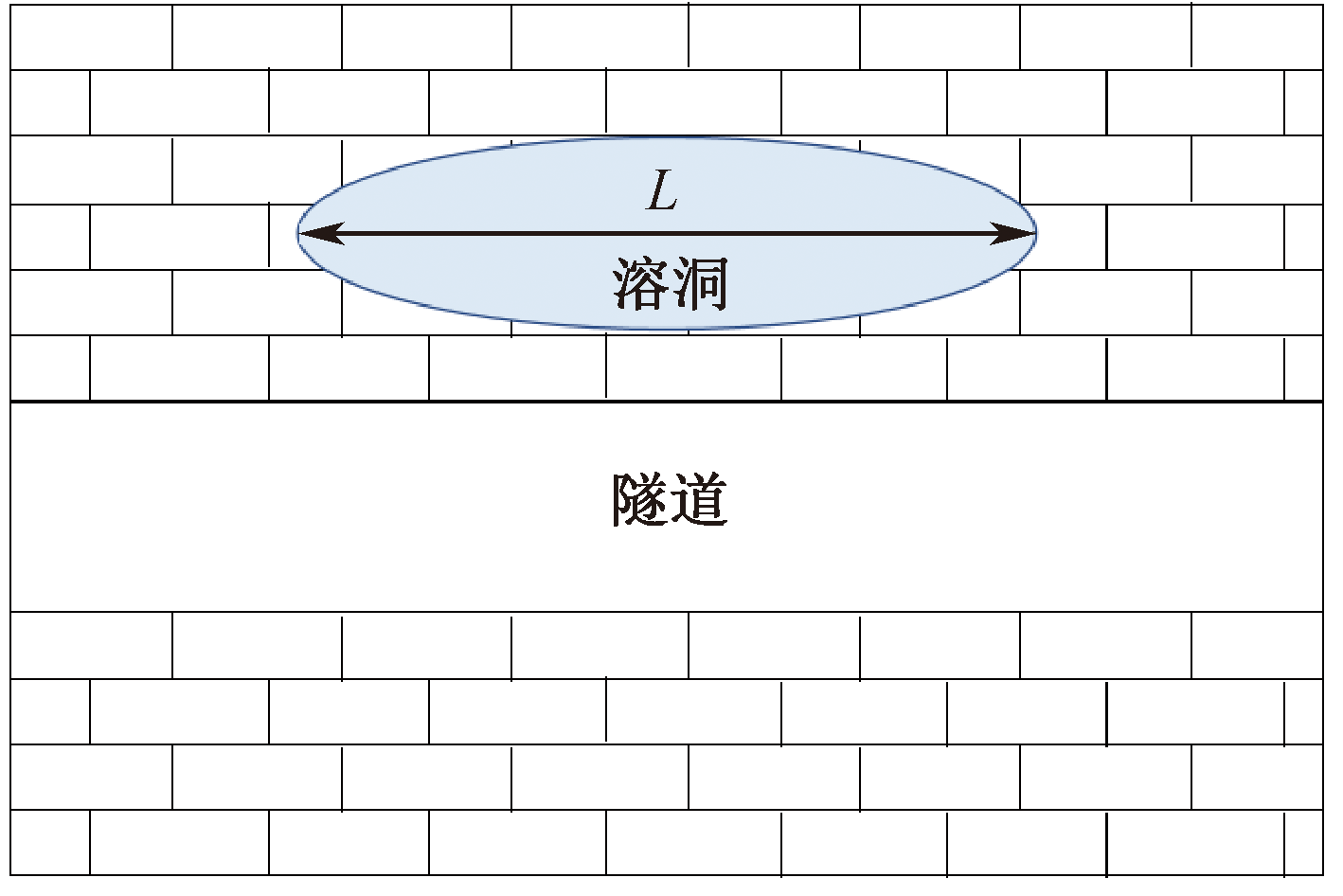
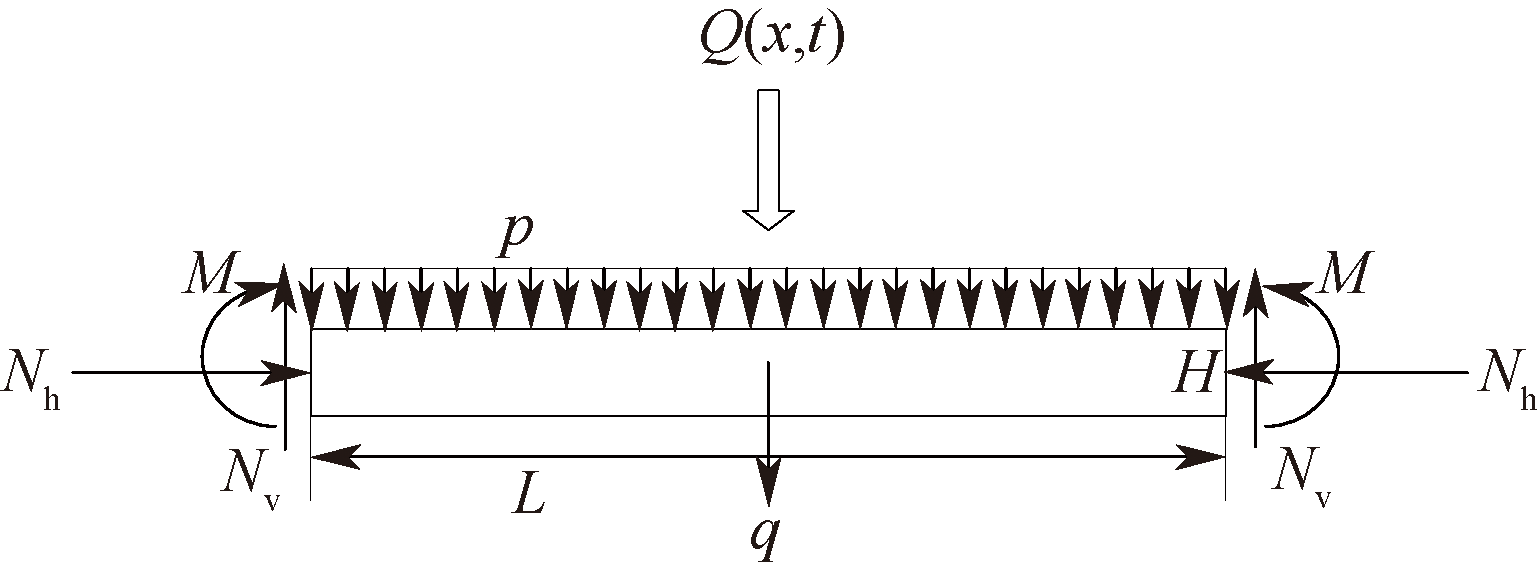
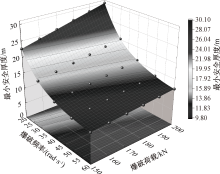
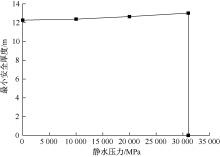
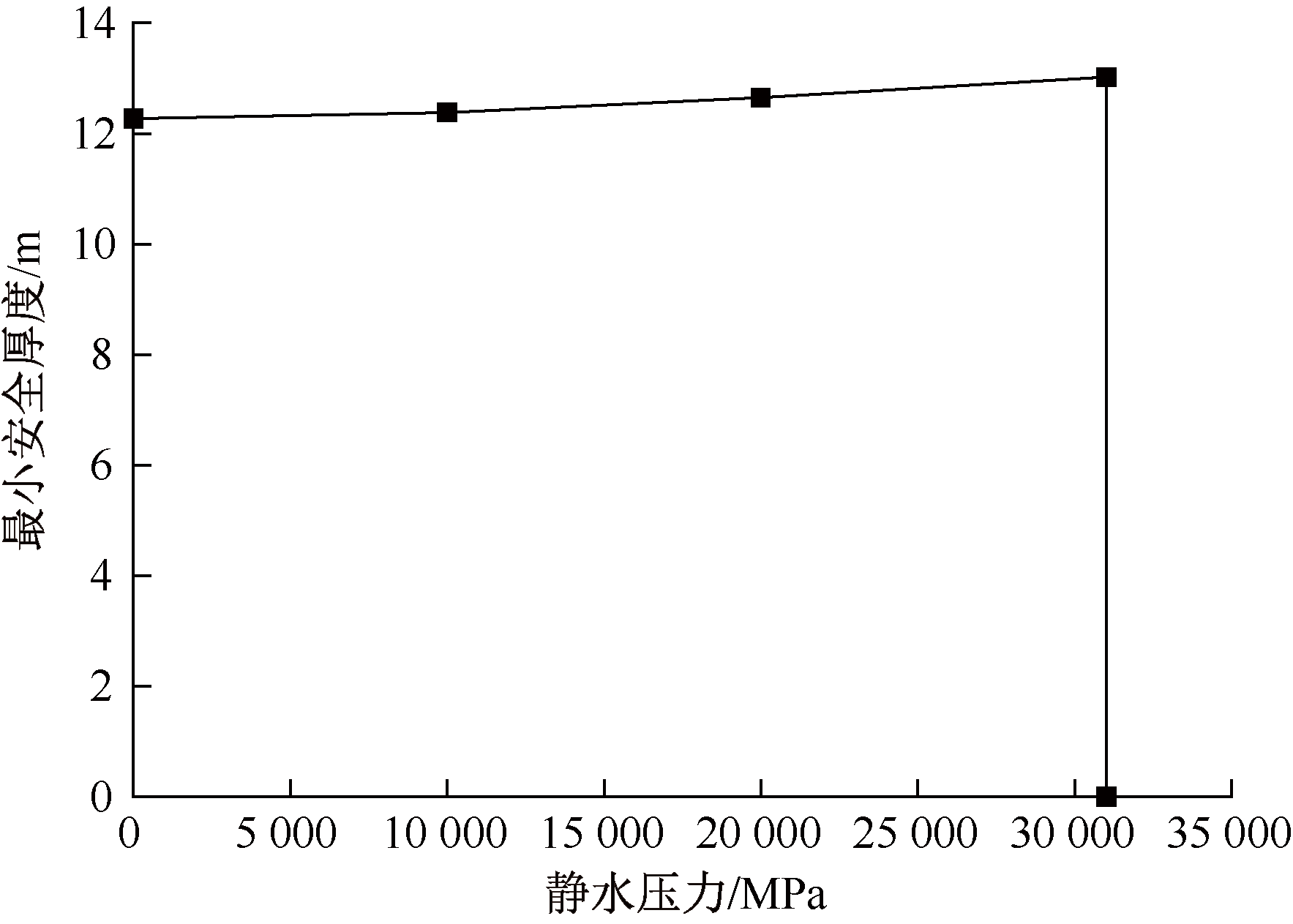
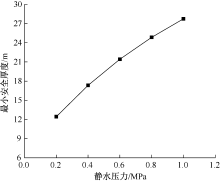
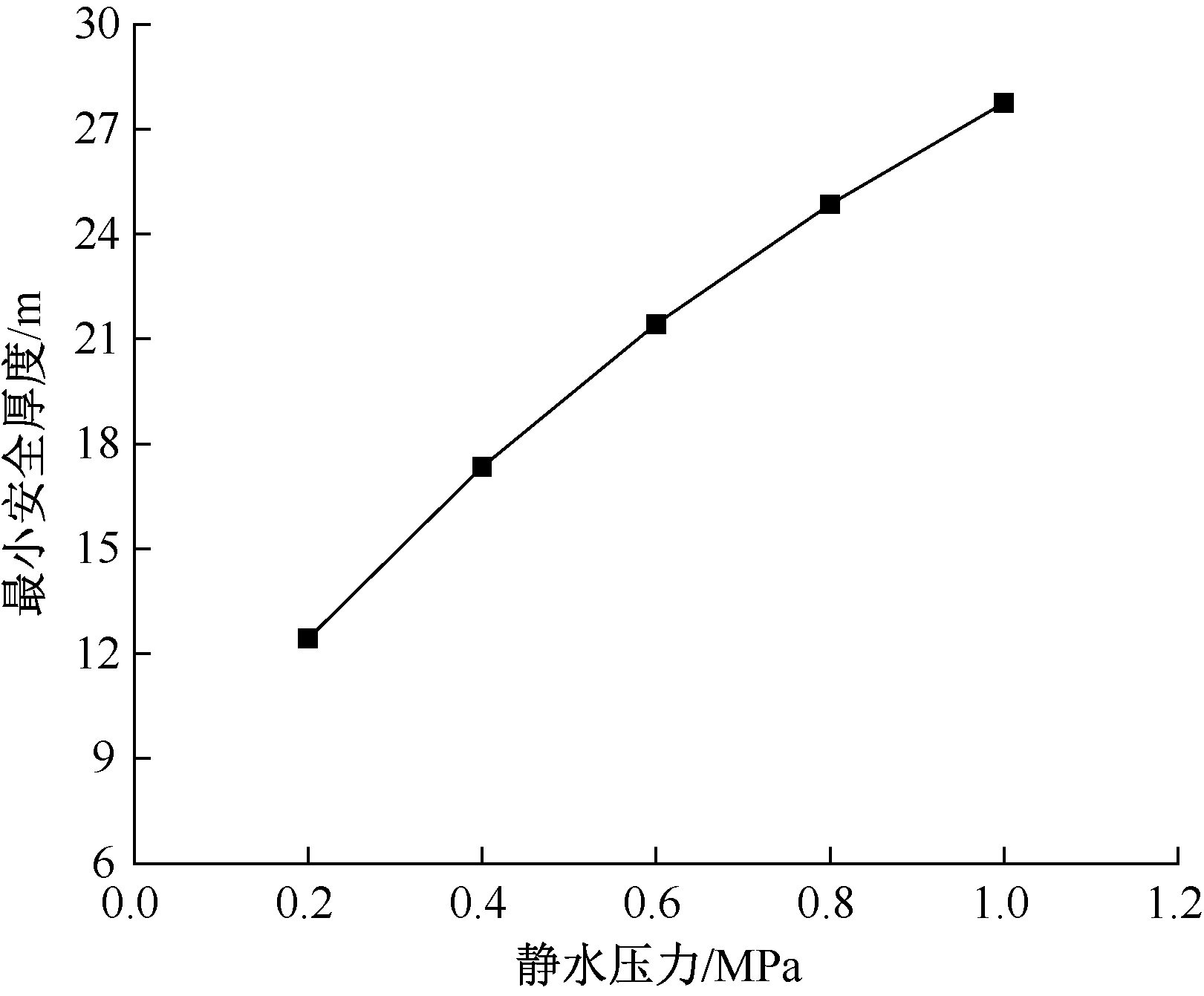
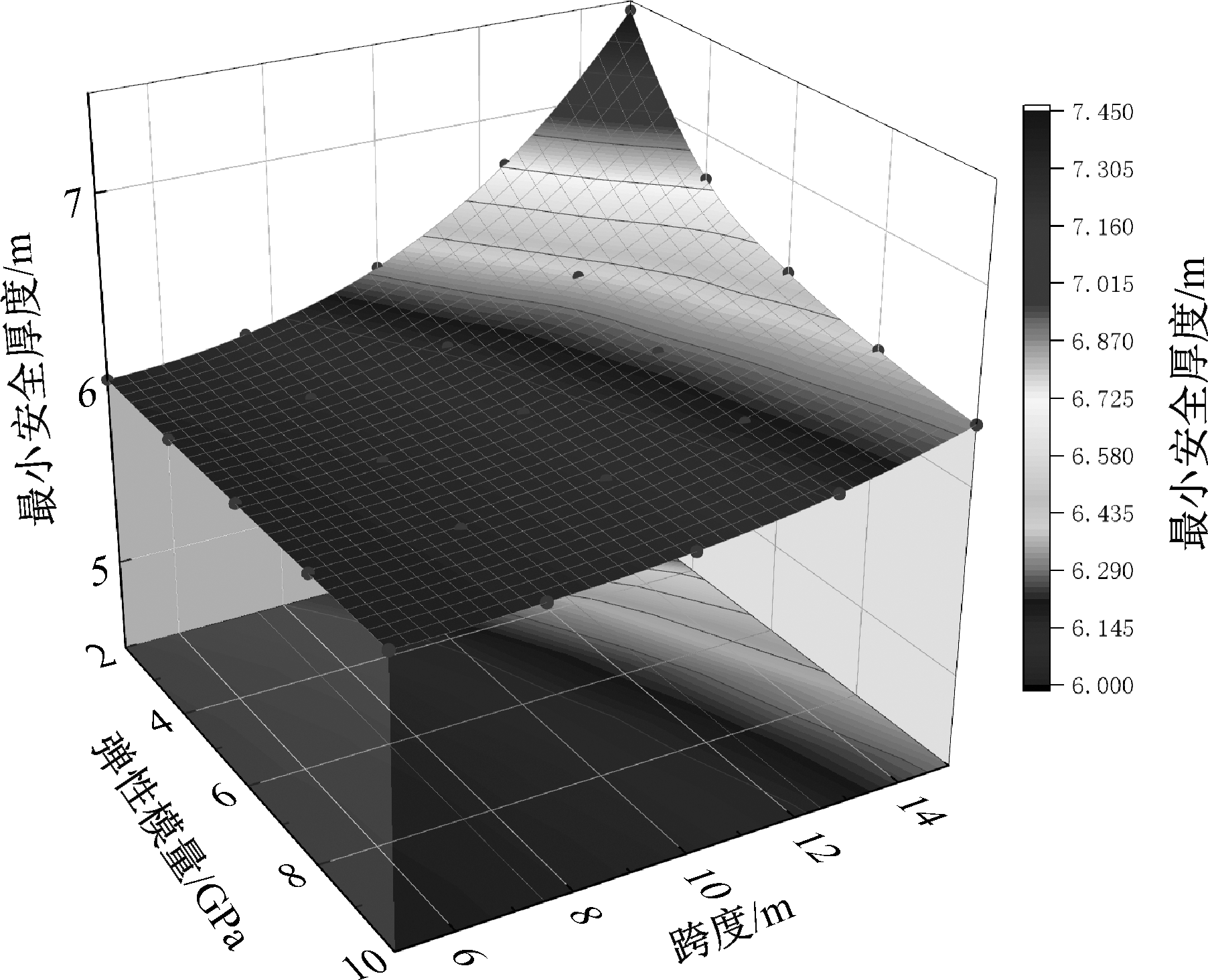
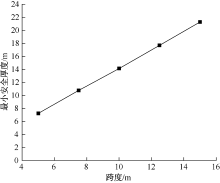
| [1] |
刘波, 肖红飞. 隧道下伏溶洞顶板安全厚度确定方法[J]. 中国安全科学学报, 2019, 29(4): 104-111.
doi: 10.16265/j.cnki.issn1003-3033.2019.04.017
|
|
LIU Bo, XIAO Hongfei. Method for determining safe thickness of cave roofs under a tunnel[J]. China Safety Science Journal, 2019, 29(4): 104-111.
doi: 10.16265/j.cnki.issn1003-3033.2019.04.017
|
| [2] |
邹洋, 彭立敏, 张智勇, 等. 基于突变理论的岩溶隧道拱顶安全厚度分析与失稳预测[J]. 铁道科学与工程学报, 2021, 18(10): 2651-2659.
|
|
ZOU Yang, PENG Limin, ZHANG Zhiyong, et al. Safety thickness analysis and stability prediction of tunnel roof in karst region based on catastrophe theory[J]. Journal of Railway Science and Engineering, 2021, 18(10): 2651-2659.
|
| [3] |
YANG Xiaoli, XIAO Haibo. Safety thickness analysis of tunnel floor in karst region based on catastrophe theory[J]. Journal of Central South University, 2016, 23(9): 2364-2372.
doi: 10.1007/s11771-016-3295-6
|
| [4] |
戴自航, 范夏玲, 卢才金. 岩溶区高速公路路堤及溶洞顶板稳定性数值分析[J]. 岩土力学, 2014, 35(增1): 382-390.
|
|
DAI Zihang, FAN Xialing, LU Caijin. Numerical analysis of stability of highway embankments and karst cave roofs in karst region[J]. Rock and Soil Mechanics, 2014, 35(S1): 382-390.
|
| [5] |
张华伟, 谢妮, 刘孔科, 等. 高层建筑桩基荷载下溶洞顶板的安全厚度[J]. 科学技术与工程, 2017, 17(32): 165-173.
|
|
ZHANG Huawei, XIE Ni, LIU Kongke, et al. Safe thickness of roof of karst cave under pilefoundation load in high-rise buildings[J]. Science, Technology and Engineering, 2017, 17(32): 165-173.
|
| [6] |
高峰, 周科平, 胡建华, 等. 充填体下矿体开采安全顶板厚度数学预测模型[J]. 岩土力学, 2008, 29 (1): 177-181.
|
|
GAO Feng, ZHOU Keping, HU Jianhua, et al. Mathematical forecasting model of safety thickness of roof for mining ore body under the complicated backfilling[J]. Rock and Soil Mechanics, 2008, 29(1): 177-181.
|
| [7] |
赖永标. 隐伏溶洞与隧道间安全距离及其智能预测模型研究[D]. 北京: 北京交通大学, 2012.
|
|
LAI Yongbiao. Study on safe distance between concealed karst cave and tunnel and its intelligent prediction model[D]. Beijing: Beijing Jiaotong University, 2012.
|
| [8] |
闫长斌, 徐国元. 动荷载诱发上下交叠硐室间顶柱失稳的突变理论分析[J]. 工程力学, 2007, 24(4): 46-51.
|
|
YAN Changbin, XU Guoyuan. Analysis on instability of the top pillar between overlap underground chambers induced by dynamic loadings with catastrophe theory[J]. Engineering Mechanics, 2007, 24(4): 46-51.
|
| [9] |
左宇军, 李夕兵, 马春德, 等. 动静组合载荷作用下岩石失稳破坏的突变理论模型与试验研究[J]. 岩石力学与工程学报, 2005, 24(5):741-746.
|
|
ZUO Yujun, LI Xibing, MA Chunde, et al. Catastrophe theory model and experimental study of rock instability failure under combined dynamic and static loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(5): 741-746.
|
| [10] |
左宇军, 李术才, 秦泗凤, 等. 动力扰动诱发承压水底板关键层失稳的突变理论研究[J]. 岩土力学, 2010, 31(8): 2361-2366.
|
|
ZUO Yujun, LI Shucai, QIN Sifeng, et al. A catastrophe model for floor water-resisting key stratum instability induced by dynamic disturbance[J]. Rock and Soil Mechanics, 2010, 31(8): 236-2362.
|
| [11] |
YANG Xiaoli, LI Zhengwei, LIU Zhengan, et al. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media[J]. Journal of Central South University, 2017, 24(4): 957-966.
doi: 10.1007/s11771-017-3498-5
|
| [12] |
江学良. 岩石地下洞室与边坡相互影响研究[D]. 长沙: 中南大学, 2008.
|
|
JIANG Xueliang. Study on interaction of rock underground cavern and slope[D]. Changsha: Central South University, 2008.
|
| [13] |
沈茂山, 魏德敏. 弹性拱振动失稳的突变模型[J]. 应用数学和力学, 1990, 11(12): 1099-1102.
|
|
SHEN Maoshan, WEI Demin. A catastrophic model for vibrational buckling of elastic arches[J]. Applied Mathematics and Mechanics, 1990, 11(12): 1 099 -1 102.
doi: 10.1007/BF02014535
|
| [14] |
张我华, 邱战洪, 陈合龙. 堤坝和基础非线性动力失稳灾变的分岔突变分析[J]. 浙江大学学报: 工学版, 2007, 41(1): 88-96.
|
|
ZHANG Wohua, QIU Zhanhong, CHEN Helong. Bifurcation and catastrophe analysis of non-linear dynamic instability disaster for dam and foundation system[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(1): 88-96.
|
| [15] |
曹茜. 岩溶隧道与溶洞的安全距离研究[D]. 北京: 北京交通大学, 2010.
|
|
CAO Qian. Study on safe thickness for rock between tunnel and karst in karst region[D]. Beijing: Beijing Jiaotong University, 2010.
|